Single Layer Perceptron

Perceptron is known as single-layer perceptron, it’s an artificial neuron using step function for activation to produces binary output, usually used to classify the data into two parts. therefore, it is also known as a Linear Binary Classifier.
Perceptron is not new, it was proposed by American psychologist Frank Rosenblatt in the 1957, based on an original McCullock-Pitts (MCP) neuron.
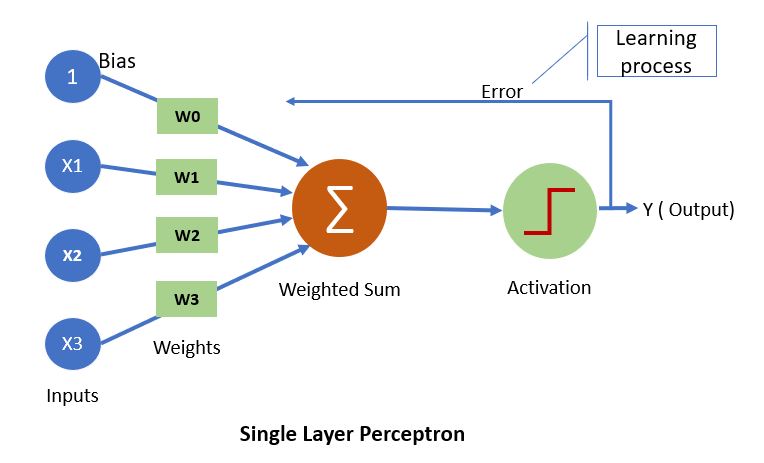
The picture shows three binary inputs (x1, x2, x3) and the output of the network is computed based on various weights (w1, w2, w3) which signify the relation between each input node and the output node. The output of the network will be 0 or 1 based on the weighted sum is less than or greater than some threshold value (which is also a real number and a parameter to the neuron).
The bias allows an activated function (threshold-based classifier) to shift the decision boundary left or right. In absence of bias, the neuron may not be activated by considering only the weighted sum from input layer. If the neuron is not activated, the information from this neuron are not passed. In summary, bias helps in controlling the value at which activation function will trigger.
Weights shows the strength of the node. we will not initialize all the weights to be zero because neuron performs the same calculation, giving the same output. All the inputs x are multiplied with their weights w and add all the multiplied values, which is called Weighted Sum.
Learning rate is a hyper-parameter that controls how much we are adjusting the weights of our network with respect the loss gradient. If learning rate is too small gradient descent can be slow and If learning rate is fast gradient descent can overshoot the minimum. It may fail to converge, it may even diverge
The step function [Heaviside] is typically used in single-layer perceptron for classification where the input data is linearly separable. The multi-layer perceptron’s can distinguish data that is not linearly, which are trained using backpropagation, needs differentiable activation function because backpropagation uses gradient descent to update the network weights.
This step function is non-differentiable at x = 0 and its derivative is 0 elsewhere, means gradient descent won’t be able to make progress in updating the weights and backpropagation will fail. The sigmoid or logistic function does not have this shortcoming and this why its been used extensively in the field of neural networks.
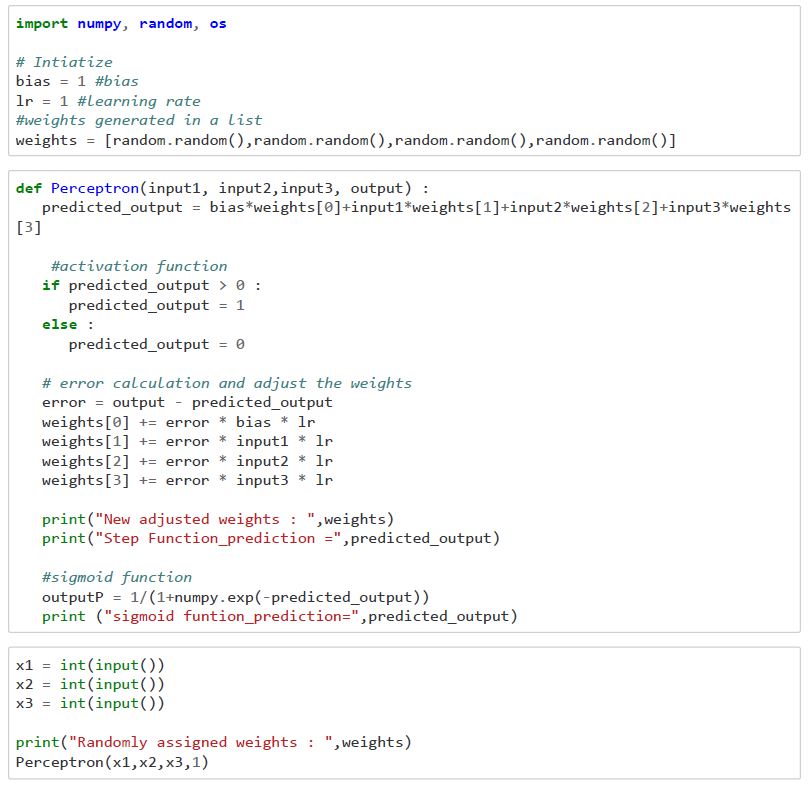
Now we understood key parts of single layer neuron, lets look at the python code illustration of perceptron.